Factorising Notes

Numbers have factors. For example, 6= 2×3. 2 and 3 are the factors of 6. What about if we have algebra instead of numbers? Expressions like $$x^2+3x+2$$ also have factors. They are $$(x+1) \text{ and } (x+2)$$ (we will cover how we find these factors with a step by step method later on).

Now that we know what factors are, what does factorising mean? Factorising is the process of finding factors.  In other words, factorising is finding what multiplies together in order to get an expression. Factorising simply “splits an expression” into a multiplication of simpler expressions. It is the direct opposite of expanding i.e. you need to turn an expression into brackets that are multiplied together. For example, splitting the expression $$x^2+3x+2$$ into $$(x+1)(x+2)$$ We know this is true since if we expand \((x+1)(x+2)\) we end up with \(x^2+3x+2\).

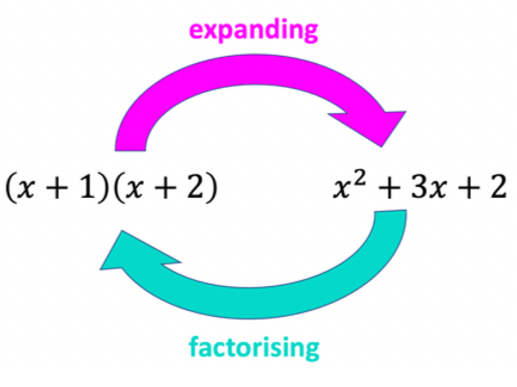
So, with factorising, once we have put our expression in brackets (in the form of a product) we are done. It’s not that easy to find these factors on our own though! It is a bit like baking a cake. Think of expanding as putting all the ingredients together to make a nice cake and factorising as having the nice cake already made and having to figure which ingredients were used to make the cake. It’s much easier to build the cake when given the ingredients, right?

You should not be scared of factorising because if you expand your answer and it’s the same as the original question, you know whether or not you’ve factorised correctly! For example, if we expand our answer above of $$(x+1)(x+2)$$ we get back the original question that we were trying to factorise, which is $$x^2+3x+2$$.

How do we factorise and what are the types of factorising? For a detailed explanation and step by step method click the buy button.